Alfa Cronbach, Prueba de regresión lineal, Prueba T, Chi cuadrada & Coeficiente de correlación de Pearson

Alfa Cronbach

El método de consistencia interna basado en el alfa de Cronbach permite estimar la fiabilidad de un instrumento de medida a través de un conjunto de ítems que se espera que midan el mismo constructo o dimensión teórica. 

La validez de un instrumento se refiere al grado en que el instrumento mide aquello que pretende medir. Y la fiabilidad de la consistencia interna del instrumento se puede estimar con el alfa de Cronbach. La medida de la fiabilidad mediante el alfa de Cronbach asume que los ítems (medidos en escala tipo Likert) miden un mismo constructo y que están altamente correlacionados (Welch & Comer, 1988). Cuanto más cerca se encuentre el valor del alfa a 1 mayor es la consistencia interna de los ítems analizados. La fiabilidad de la escala debe obtenerse siempre con los datos de cada muestra para garantizar la medida fiable del constructo en la muestra concreta de investigación. 

Como criterio general, George y Mallery (2003, p. 231) sugieren las recomendaciones siguientes para evaluar los coeficientes de alfa de Cronbach: 

-Coeficiente alfa >.9 es excelente 

- Coeficiente alfa >.8 es bueno 

-Coeficiente alfa >.7 es aceptable 

- Coeficiente alfa >.6 es cuestionable 

- Coeficiente alfa >.5 es pobre 

- Coeficiente alfa <.5 es inaceptable 

Valoraciones de los autores: 

* Nunnally (1967, p. 226): en las primeras fases de la investigación un valor de fiabilidad de 0.6 o 0.5 puede ser suficiente. Con investigación básica se necesita al menos 0.8 y en investigación aplicada entre 0.9 y 0.95. 

* Nunnally (1978, p.245-246): dentro de un análisis exploratorio estándar, el valor de fibilidad en torno a 0.7 es adecuado. 

* Kaplan & Saccuzzo (1982, p. 106): el valor de fiabilidad para la investigación básica entre 0.7 y 0.8; en investigación aplicada sobre 0.95. 

* Loo (2001, p. 223): el valor de consistencia que se considera adecuado es de 0.8 o más. 

* Gliem & Gliem (2003): un valor de alfa de 0.8 es probablemente una meta razonable. 

* Huh, Delorme & Reid (2006): el valor de fiabilidad en investigación exploratoria debe ser igual o mayor a 0.6; en estudios confirmatorios debe estar entre 0.7 y 0.8.

PRUEBA DE REGRESIÓN LINEAL 

es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente Y, las variables independientes X_i y un término aleatorio ε. Este modelo puede ser expresado como:

${\displaystyle Y_{t}=\beta _{0}+\beta _{1}X_{1}+\beta _{2}X_{2}+\cdots +\beta _{p}X_{p}+\varepsilon }$

 Donde:

: variable dependiente, explicada o regresando.
: variables explicativas, independientes o regresores.
: parámetros, miden la influencia que las variables explicativas tienen sobre el regrediendo.

donde ${\displaystyle \beta _{0}}$ es la intersección o término "constante", las ${\displaystyle \beta _{i}\ (i>0)}$ son los parámetros respectivos a cada variable independiente, y ${\displaystyle p}$ es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.

El modelo de regresión lineal relaciona la variable dependiente Y con K variables explícitas  (k = 1,...K), o cualquier transformación de éstas que generen un hiperplano de parámetros desconocidos:

   

${\displaystyle Y=\sum \beta _{k}X_{k}+\varepsilon }$

donde ${\displaystyle \varepsilon }$ es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explícita, el hiperplano es una recta: 

${\displaystyle Y=\beta _{1}+\beta _{2}X_{2}+\varepsilon }$

El problema de la regresión consiste en elegir unos valores determinados para los parámetros desconocidos ${\displaystyle \beta _{k}}$, de modo que la ecuación quede completamente especificada. Para ello se necesita un conjunto de observaciones. En una observación i-ésima (i= 1,... I) cualquiera, se registra el comportamiento simultáneo de la variable dependiente y las variables explícitas (las perturbaciones aleatorias se suponen no observables).

${\displaystyle Y_{i}=\sum \beta _{k}X_{ki}+\varepsilon _{i}}$

Los valores escogidos como estimadores de los parámetros ${\displaystyle {\hat {\beta _{k}}}}$, son los coeficientes de regresión sin que se pueda garantizar que coincida n con parámetros reales del proceso generador. Por tanto, en

${\displaystyle Y_{i}=\sum {\hat {\beta _{k}}}X_{ki}+{\hat {\varepsilon _{i}}}}$

Los valores ${\displaystyle {\hat {\varepsilon _{i}}}}$ son por su parte estimaciones o errores de la perturbación aleatoria.

Tipos de regresión lineal

Regresión lineal simple: 

Sólo se maneja una variable independiente, por lo que sólo cuenta con dos parámetros. Son de la forma:

${\displaystyle Y_{i}=\beta _{0}+\beta _{1}X_{i}+\varepsilon _{i}}$

donde ${\displaystyle \varepsilon _{i}}$ es el error asociado a la medición del valor ${\displaystyle X_{i}}$ y siguen los supuestos de modo que ${\displaystyle \varepsilon _{i}\sim N(0,\sigma ^{2})}$ (media cero, varianza constante e igual a un ${\displaystyle \sigma }$ y ${\displaystyle \varepsilon _{i}\perp \varepsilon _{j}}$ con ${\displaystyle i\neq j}$).

Dado el modelo de regresión simple anterior, si se calcula la esperanza (valor esperado) del valor Y, se obtiene:

Derivado respecto a ${\displaystyle {\hat {\beta }}_{0}}$ y ${\displaystyle {\hat {\beta }}_{1}}$ e igualando a cero, se obtiene:

Obteniendo dos ecuaciones denominadas ecuaciones normales que generan la siguiente solución para ambos parámetros:

 La interpretación del parámetro medio  es que un incremento en Xi de una unidad, Yi incrementará en 

Regresión lineal múltiple

Las rectas de regresión son las rectas que mejor se ajustan a la nube de puntos (o también llamado diagrama de dispersión) generada por una distribución binomial. Matemáticamente, son posibles dos rectas de máximo ajuste:

• La recta de regresión de Y sobre X:

• La recta de regresión de X sobre Y:

 La correlación ("r") de las rectas determinará la calidad del ajuste. Si r es cercano o igual a 1, el ajuste será bueno y las predicciones realizadas a partir del modelo obtenido serán muy fiables (el modelo obtenido resulta verdaderamente representativo); si r es cercano o igual a 0, se tratará de un ajuste malo en el que las predicciones que se realicen a partir del modelo obtenido no serán fiables (el modelo obtenido no resulta representativo de la realidad). Ambas rectas de regresión se intersecan en un punto llamado centro de gravedad de la distribución.

El procedimiento Prueba T para muestras independientes compara las medias de dos grupos de casos. Lo ideal es que para esta prueba los sujetos se asignen aleatoriamente a dos grupos, de forma que cualquier diferencia en la respuesta sea debida al tratamiento (o falta de tratamiento) y no a otros factores. Este caso no ocurre si se comparan los ingresos medios para hombres y mujeres. El sexo de una persona no se asigna aleatoriamente. En estas situaciones, debe asegurarse de que las diferencias en otros factores no enmascaren o resalten una diferencia significativa entre las medias. Las diferencias de ingresos medios pueden estar sometidas a la influencia de factores como los estudios (y no solamente el sexo).

Ejemplo. Se asigna aleatoriamente un grupo de pacientes con hipertensión arterial a un grupo con placebo y otro con tratamiento. Los sujetos con placebo reciben una pastilla inactiva y los sujetos con tratamiento reciben un nuevo medicamento del cual se espera que reduzca la tensión arterial. Después de tratar a los sujetos durante dos meses, se utiliza la prueba t para dos muestras para comparar la tensión arterial media del grupo con placebo y del grupo con tratamiento. Cada paciente se mide una sola vez y pertenece a un solo grupo.

Estadísticos. Para cada variable: tamaño de la muestra, media, desviación estándar y error estándar de la media. Para la diferencia entre las medias: media, error estándar e intervalo de confianza (puede especificar el nivel de confianza). Pruebas: prueba de Levene sobre la igualdad de varianzas y pruebas t de varianzas combinadas y separadas sobre la igualdad de las medias.

Prueba T para muestras independientes: Consideraciones sobre los datos

Datos. Los valores de la variable cuantitativa de interés se hallan en una única columna del archivo de datos. El procedimiento utiliza una variable de agrupación con dos valores para separar los casos en dos grupos. La variable de agrupación puede ser numérica (valores como 1 y 2, o 6,25 y 12,5) o de cadena corta (como sí y no). También puede usar una variable cuantitativa, como la edad, para dividir los casos en dos grupos especificando un punto de corte (el punto de corte 21 divide la edad en un grupo de menos de 21 años y otro de más de 21).

Supuestos. Para la prueba t de igualdad de varianzas, las observaciones deben ser muestras aleatorias independientes de distribuciones normales con la misma varianza de población. Para la prueba t de varianzas desiguales, las observaciones deben ser muestras aleatorias independientes de distribuciones normales. La prueba t para dos muestras es bastante robusta a las desviaciones de la normalidad. Al contrastar las distribuciones gráficamente, compruebe que son simétricas y que no contienen valores atípicos.

Para obtener una prueba T para muestras independientes

Esta característica requiere la opción Statistics Base.

1. Seleccione en los menús:
   Analizar > Comparar medias > Prueba T para muestras independientes...                    
2. Seleccione una o más variables de contraste cuantitativas. Se calcula una prueba t para cada variable.
3. Seleccione una sola variable de agrupación y pulse en definir grupos para especificar dos códigos para los grupos que desee comparar.
4. Si lo desea, puede pulsar en opciones para controlar el tratamiento de los datos perdidos y el nivel del intervalo de confianza.

Chi cuadrado

Esta prueba puede utilizarse incluso con datos medibles en una escala nominal. La hipótesis nula de la prueba Chi-cuadrado postula una distribución de probabilidad totalmente especificada como el modelo matemático de la población que ha generado la muestra.

Para realizar este contraste se disponen los datos en una tabla de frecuencias. Para cada valor o intervalo de valores se indica la frecuencia absoluta observada o empírica (Oi). A continuación, y suponiendo que la hipótesis nula es cierta, se calculan para cada valor o intervalo de valores la frecuencia absoluta que cabría esperar o frecuencia esperada (Ei=n·pi , donde n es el tamaño de la muestra y pi la probabilidad del i-ésimo valor o intervalo de valores según la hipótesis nula). El estadístico de prueba se basa en las diferencias entre la Oi y Ei y se define como:

Este estadístico tiene una distribución Chi-cuadrado con k-1 grados de libertad si n es suficientemente grande, es decir, si todas las frecuencias esperadas son mayores que 5. En la práctica se tolera un máximo del 20% de frecuencias inferiores a 5.

Si existe concordancia perfecta entre las frecuencias observadas y las esperadas el estadístico tomará un valor igual a 0; por el contrario, si existe una gran discrepancias entre estas frecuencias el estadístico tomará un valor grande y, en consecuencia, se rechazará la hipótesis nula. Así pues, la región crítica estará situada en el extremo superior de la distribución Chi-cuadrado con k-1 grados de libertad.

Para realizar un contraste Chi-cuadrado la secuencia es:

Analizar

Pruebas no paramétricas

Chi-cuadrado

En el cuadro de diálogo Prueba chi-cuadrado se indica la variable a analizar en Contrastar variables.

En Valores esperados se debe especificar la distribución teórica activando una de las dos alternativas. Por defecto está activadaTodas la categorías iguales que recoge la hipótesis de que la distribución de la población es uniforme discreta. La opción Valoresrequiere especificar uno a uno los valores esperados de las frecuencias relativas o absolutas correspondientes a cada categoría, introduciéndolos en el mismo orden en el que se han definido las categorías.

El recuadro Rango esperado presenta dos opciones: por defecto está activada Obtener de los datos que realiza el análisis para todas las categorías o valores de la variable; la otra alternativa, Usar rango especificado, realiza el análisis sólo para un deteminado rango de valores cuyos límites Inferior y Superior se deben especificar en los recuadros de texto correspondientes.

El cuadro de diálogo al que se accede con el botón Opciones ofrece la posibilidad de calcular los Estadísticos Descriptivos y/o losCuartiles, así como seleccionar la forma en que se desea tratar los valores perdidos.

Coefficiente de Pearson

la covariación es el grado de concordancia de las posiciones relativas de datos de dos variables. En consecuencia el coeficiente de correlación de Pearson opera con puntuaciones tificadas (que miden posiciones relativas) y se define:

El fundamento del coeficiente de Pearon es el siguiente: Cuanto más intensa sea la concordancia (en sentido directo o inverso) de las posiciones relativas de los datos en las dos variables, el producto del numerador toma mayor valor (en sentido absoluto). si la concordancia es exacta, el numerador es igual a N (o a-N), y el indice toma un valor igual a 1 (o-1).
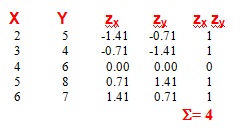
Ejemplo 1 (Máxima covariación positiva) 

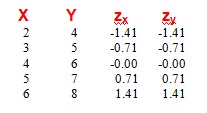
observa que los datos tificados (expresados como puntuaciones z) en las dos columnas de la derecha tienen los mismos valores en ambas variables, dado que las posiciones relativas son las mismas en las variables X e Y.
si obtenemos los productos de los valores tificados para cada caso, el resultado es:



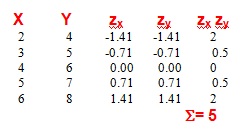
El cociente de dividir la suma de productos (5) por N (hay que tener en cuenta que N es el número de casos, NO el número de datos) es igual a 1: 







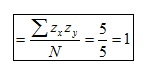
Covariación positiva de alta intensidad

por lo tanto, 

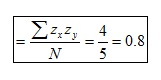
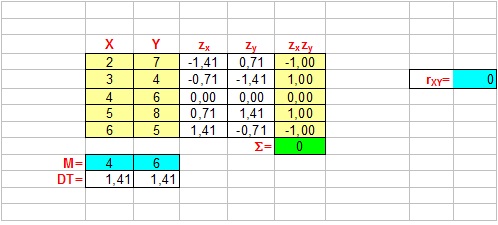
Ausencia de covariación



Covariación negativa de alta intensidad 


Máxima covariación negativa

El valor de la correlación es igual a 1 o -1 si la covariación es de intensidad máxima, y se va acercando hacia el 0 cuanto más pequeña sea la intensidad de la covariacón. Además el indice tiene signo positivo cuando la covariación es directa y negativo cuando es inversa.

Caracteristicas

* El coeficiente de correlación de Pearson puede tomar valores entre -1 y 1

* L a correlación de una variable con ella misma siempre es igual a 1

* El valor 0 indica ausencia de covariacón lineal, pero NO si la covariación es de tipo no lineal.